www.algospot.com/judge/problem/read/BOARDCOVER
algospot.com :: BOARDCOVER
게임판 덮기 문제 정보 문제 H*W 크기의 게임판이 있습니다. 게임판은 검은 칸과 흰 칸으로 구성된 격자 모양을 하고 있는데 이 중 모든 흰 칸을 3칸짜리 L자 모양의 블록으로 덮고 싶습니다. 이
www.algospot.com
흔한 완전 탐색 문제기에, 코드를 짜는 것의 난이도 자체는 높지 않다고 생각합니다. 이 문제를 풀면서 오래 걸렸던 부분이 있는데 그림으로 보여드리겠습니다.
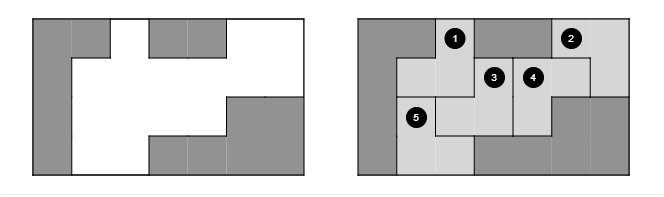
바로 가장 위쪽 그리고 왼쪽부터 탐색을 해도 모든 칸을 다 채울 수 있다는 점입니다. 가장 위 열부터 블록을 채워 나가기 때문에 좌표를 기준으로 위로 그려지는 블록은 배제할 수 있습니다.
int search()
{
int chk = 0;
int start[2];
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
if (board[i][j] == '.') {
if (!chk) {
start[0] = i;
start[1] = j;
}
chk++;
}
}
}
if (chk % 3 != 0) return 0;
total = chk / 3;
cover(start[0], start[1], 0);
return res;
}입력받은 게임판 중 블록이 놓이지 않은 부분('.')을 찾아 개수를 셉니다. 그리고 가장 먼저 나온 빈칸을 탐색 시작 지점으로 설정하겠습니다. 블록은 무조건 좌표 3칸을 차지하게 돼 있으며, 그렇기 때문에 모든 블록을 다 채우기 위해선 빈칸의 개수는 3의 배수여야 합니다. 빈칸이 3의 배수가 아닌 게임판이 입력되면 바로 예외처리를 해주시면 됩니다. 빈칸의 개수가 3의 배수라면 첫 탐색 시작 지점을 파라미터로 게임판을 덮는 함수를 실행시킵니다.
void cover(int y, int x, int cnt)
{
if (cnt == total) {
res++;
return;
}
if (board[y][x] == '#') {
return cover(y + (x + 1) / w, (x + 1) % w, cnt);
}
for (int i = 0; i < 4; i++) {
if (put(y, x, i, '#')) {
cover(y + (x + 1) / w, (x + 1) % w, cnt + 1);
put(y, x, i, '.');
}
}
return;
}시작지점부터 하여 빈칸을 채우기 시작합니다. 고려해야 할 블록의 모양은 4종류입니다. 좌표를 기준으로 그려질 수 있는 블록의 모양은 총 8개이나, 가장 위 열부터 블록을 채우기 때문에 위로 그려지는 4종류는 배제합니다. 해당 좌표에 4종류 중 놓을 수 있는 블록을 발견하면 다음 좌표를 탐색하기 위해 함수를 재귀 호출합니다. 다만 탐색지점이 블록을 둘 수 없는 칸('#')이라면 블록의 개수(cnt)는 그대로 두되 좌표만 다음 지점으로 옮겨 함수를 다시 실행합니다. 이렇게 블록을 채우며 채운 블록의 개수(cnt)와 빈칸을 모두 덮기 위한 블록의 개수(total)가 같아지면 블록을 둘 수 있는 경우의 수(res)를 증가시키고 되돌아갑니다.
int direction[4][2][2] = {
{{1, 0}, {0, 1}},
{{0, 1}, {1, 1}},
{{1, 0}, {1, 1}},
{{1, 0}, {1, -1}}
};
bool put(int y, int x, int i, char c)
{
for (int j = 0; j < 2; j++) {
int ny = y + direction[i][j][0];
int nx = x + direction[i][j][1];
if (ny >= h || nx < 0 || nx >= w) return false;
if (board[ny][nx] == c) return false;
}
board[y][x] = c;
for (int j = 0; j < 2; j++) {
int ny = y + direction[i][j][0];
int nx = x + direction[i][j][1];
board[ny][nx] = c;
}
return true;
}블록을 둘 수 있는지 체크한 후 블록을 두는 함수입니다. 블록이 게임판을 넘어가거나 둘 수 없는 지점이 생긴다면 false를 즉시 리턴합니다. 모든 조건을 통과한다면 해당 지점에 해당 모양의 블록을 덮습니다. 파라미터로 넘어온 문자(c)가 '#'이라면 블록을 덮고 '.'이라면 블록을 뺍니다.
#include<iostream>
using namespace std;
char board[20][21];
int c, h, w, res, total;
int direction[4][2][2] = {
{{1, 0}, {0, 1}},
{{0, 1}, {1, 1}},
{{1, 0}, {1, 1}},
{{1, 0}, {1, -1}}
};
bool put(int y, int x, int i, char c)
{
for (int j = 0; j < 2; j++) {
int ny = y + direction[i][j][0];
int nx = x + direction[i][j][1];
if (ny >= h || nx < 0 || nx >= w) return false;
if (board[ny][nx] == c) return false;
}
board[y][x] = c;
for (int j = 0; j < 2; j++) {
int ny = y + direction[i][j][0];
int nx = x + direction[i][j][1];
board[ny][nx] = c;
}
return true;
}
void cover(int y, int x, int cnt)
{
if (cnt == total) {
res++;
return;
}
if (board[y][x] == '#') {
return cover(y + (x + 1) / w, (x + 1) % w, cnt);
}
for (int i = 0; i < 4; i++) {
if (put(y, x, i, '#')) {
cover(y + (x + 1) / w, (x + 1) % w, cnt + 1);
put(y, x, i, '.');
}
}
return;
}
int search()
{
int chk = 0;
int start[2];
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
if (board[i][j] == '.') {
if (!chk) {
start[0] = i;
start[1] = j;
}
chk++;
}
}
}
if (chk % 3 != 0) return 0;
total = chk / 3;
cover(start[0], start[1], 0);
return res;
}
int main(void)
{
cin >> c;
for (int i = 0; i < c; i++) {
cin >> h >> w;
for (int j = 0; j < h; j++) {
cin >> board[j];
}
res = 0;
cout << search() << endl;
}
return 0;
}재귀 호출을 통한 완전 탐색으로 어렵지 않게 구현할 수 있는 문제입니다. 하지만 처음에도 말했듯이 가장 위 열, 그리고 가장 왼쪽 칸부터 블록을 두어도 모든 경우의 수를 고려할 수 있다는 점을 알아채기가 조금 어려웠던 문제였습니다.
'알고리즘 > 알고스팟' 카테고리의 다른 글
| [알고스팟/C,C++] QUADTREE: 쿼드 트리 뒤집기 (0) | 2021.03.27 |
|---|---|
| [알고스팟/C,C++] CLOCKSYNK: Synchronizing Clocks (0) | 2021.03.15 |
| [알고스팟/C,C++] PICNIC: 소풍 (0) | 2021.03.09 |
| [알고스팟/C,C++] BOGGLE: 보글 게임 (1) | 2021.03.08 |
| [알고스팟/C,C++] FESTIVAL: 록 페스티벌 (0) | 2021.03.08 |


댓글